There is an insanely cool, simple and elegant way to calculate Fibonacci numbers in assembly using only 2 opcodes! Full disclosure: this post is inspired by chapter two of the book “xchg rax, rax”.
Fibonacci Numbers
Just a simple review: Fibonacci Numbers are calculated with the formula below.
So for example to get the 3’rd Fibonacci number, we need to sum the 2nd and 1st Fibonacci numbers.
The Code
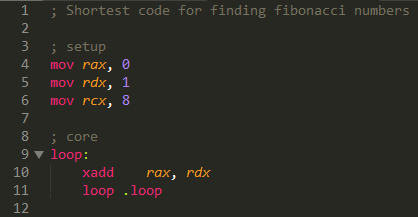
Behold! Below is the most elegant code you will ever see for in assembly
Source available here.
Explanation
The magic happens in the XADD opcode which is an “xchg (exchange)” and “add” operation in one opcode. It works exactly as you would expect: first exchange the two operands, and then add them saving the result to the first operand. Official Intel documentation here.
Next, the “loop” opcode changes the code flow to jump back and re-execute the xadd opcode multiple times.
Understanding
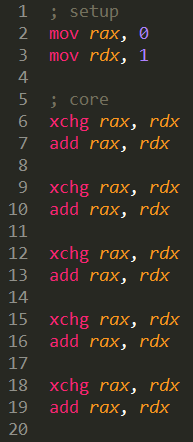
To completely understand why and how this compact works lets further break it down. Let’s expand the xadd opcode to two separate xchg and add opcodes. Secondly, let’s unroll the loop in the code by writing our loop body multiple times. Expanded code
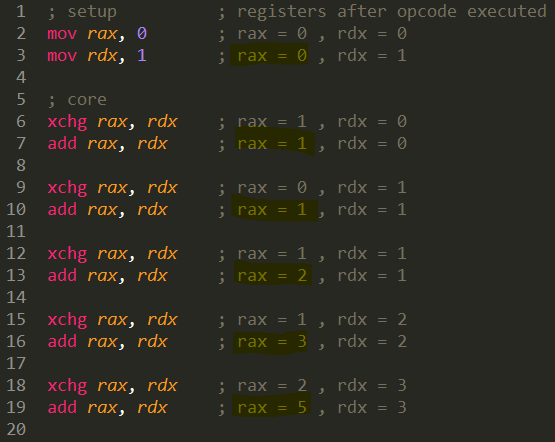
Now that the code is simplified, let’s simulate a processor and review each register’s value after each opcode.
Notice that the highlighted value in RAX after every add has the correct Fibonacci number. The first iteration (the setup) RAX has 0 - the first Fibonacci number. The second iteration RAX has 1 - the second Fibonacci number. And so on and so forth until our example stops at the 6th iteration where RAX has 5 - the sixths Fibonacci number.
Closing Note
I personally really enjoy these assembly riddles as they require you to think very critically. If you also enjoy these types of riddles, or some might even consider it poetry, I highly recommend you buy the “xchg rax, rax” book (this is not sponsored). If you currently can’t afford the book, there is a free online version here.
If you want to see more of these types of posts, let me know! Follow me on twitter for the latest updates.